TIL Matematica – Demo
0 di 8 domande completate
Domande:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
Informazione
|
Bisogna indicare un indirizzo email |
|
|
Bisogna riempire questo campo |
Stai per iniziare la simulazione della sezione di Matematica del TIL-I (Test in Laib – Ingegneria) del Politecnico di Torino.
Questa versione dimostrativa si compone di 8 domande da svolgere in 18 minuti.
Ti ricordiamo che invece la prova completa di Matematica del TIL-I dura 36 minuti ed è composta da 16 domande.
Puoi esercitarti con le simulazioni complete e le correzioni dettagliate del Corso Completo TIL POLITO
Durante la prova potrai rivedere le domande a cui hai già dato risposta. Allo scadere del tempo, il test si concluderà automaticamente mostrandoti le risposte ai quesiti.
Assicurati di essere in un ambiente tranquillo in quanto non sarà possibile interrompere lo svolgimento se non terminando e iniziando nuovamente la prova.
Premi il tasto sottostante per iniziare la prova.
Hai già completato il quiz pertanto non puoi rifarlo.
Il quiz si sta caricando…
Devi iscriverti o registrarti per iniziare il quiz.
Bisogna completare il seguente quiz per poter avviare questo quiz:
Risultati
0 di 8 domande risposte correttamente
Il tuo tempo:
Il tempo è scaduto
Punteggio finale: 0
Risposte fornite: 0
Risposte corrette: 0 con punteggio 0
Risposte non corrette: 0 con penalità 0
| Punteggio medio |
|
| Il tuo punteggio |
|
-
Non categorizzato
Risposte fornite: 0
Risposte corrette: 0 con punteggio 0
Risposte non corrette: 0 con punteggio 0
-
Vuoi metterti alla prova con altre simulazioni per prepararti e ripassare ciò che c’è da sapere per superare rapidamente l’esame? Continua ad esercitarti con le simulazioni complete e le correzioni dettagliate:
Vai al Corso Completo TIL POLITO
Leggi le opinioni degli altri studenti o contattaci per qualsiasi informazione. Consulta anche la pagina dei Codici Sconto per verificare le promozioni disponibili.
Premi il tasto sottostante per vedere le correzioni.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- Risposta
- Controlla
-
Domanda 1 di 8
1. Domanda
Uno studente dice di essere riuscito a trovare un valore tale per cui:
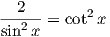
Allora:
Corretto
Soluzione : C. Essendo la cotangente il rapporto fra coseno e seno, si può notare che per sin(x)≠0, il denominatore è semplificabile. L’equazione goniometrica rimanente è cos2(x) = 2. Essendo il coseno sempre compreso tra -1 e 1, il suo quadrato sarà compreso tra 0 e 1 (in quanto i suoi valori negativi, al quadrato, diventano positivi) e quindi mai uguale 2.
Non corretto
Soluzione : C. Essendo la cotangente il rapporto fra coseno e seno, si può notare che per sin(x)≠0, il denominatore è semplificabile. L’equazione goniometrica rimanente è cos2(x) = 2. Essendo il coseno sempre compreso tra -1 e 1, il suo quadrato sarà compreso tra 0 e 1 (in quanto i suoi valori negativi, al quadrato, diventano positivi) e quindi mai uguale 2.
Risposta non fornita
Soluzione : C. Essendo la cotangente il rapporto fra coseno e seno, si può notare che per sin(x)≠0, il denominatore è semplificabile. L’equazione goniometrica rimanente è cos2(x) = 2. Essendo il coseno sempre compreso tra -1 e 1, il suo quadrato sarà compreso tra 0 e 1 (in quanto i suoi valori negativi, al quadrato, diventano positivi) e quindi mai uguale 2.
-
Domanda 2 di 8
2. Domanda
Qual è la soluzione della seguente equazione?
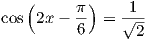 Corretto
Corretto
Soluzione: D. Notando che il coseno assume il valore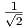 per angoli uguali a π⁄4 + 2kπ ed a 7⁄4π + 2kπ, si deve avere che 2x –π⁄6 = π⁄4 + 2kπ e che 2x –π⁄6 = 7⁄4π + 2kπ, da cui si ottiene
per angoli uguali a π⁄4 + 2kπ ed a 7⁄4π + 2kπ, si deve avere che 2x –π⁄6 = π⁄4 + 2kπ e che 2x –π⁄6 = 7⁄4π + 2kπ, da cui si ottiene
x = 5⁄24π + kπ e x = 23⁄24π + kπ
Non corretto
Soluzione: D. Notando che il coseno assume il valore
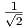 per angoli uguali a π⁄4 + 2kπ ed a 7⁄4π + 2kπ, si deve avere che 2x –π⁄6 = π⁄4 + 2kπ e che 2x –π⁄6 = 7⁄4π + 2kπ, da cui si ottiene
per angoli uguali a π⁄4 + 2kπ ed a 7⁄4π + 2kπ, si deve avere che 2x –π⁄6 = π⁄4 + 2kπ e che 2x –π⁄6 = 7⁄4π + 2kπ, da cui si ottiene
x = 5⁄24π + kπ e x = 23⁄24π + kπRisposta non fornita
Soluzione: D. Notando che il coseno assume il valore
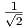 per angoli uguali a π⁄4 + 2kπ ed a 7⁄4π + 2kπ, si deve avere che 2x –π⁄6 = π⁄4 + 2kπ e che 2x –π⁄6 = 7⁄4π + 2kπ, da cui si ottiene
per angoli uguali a π⁄4 + 2kπ ed a 7⁄4π + 2kπ, si deve avere che 2x –π⁄6 = π⁄4 + 2kπ e che 2x –π⁄6 = 7⁄4π + 2kπ, da cui si ottiene
x = 5⁄24π + kπ e x = 23⁄24π + kπ -
Domanda 3 di 8
3. Domanda
Nel triangolo ABC conosciamo la bisettrice CL = l, l’angolo
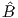 = β, l’angolo Ĉ = 2γ: vogliamo trovare i lati. Possiamo affermare che:Corretto
= β, l’angolo Ĉ = 2γ: vogliamo trovare i lati. Possiamo affermare che:Corretto
Soluzione: C. Per risolvere tale quesito è necessario ricordare che sin(π – α) = sin(α) ed il teorema dei seni, secondo cui in ogni triangolo ogni lato è proporzionale al seno dell’angolo opposto. Nel triangolo considerato è necessario tracciare la bisettrice a Ĉ che incontra il lato AB in L, formando il segmento CL = l. Il triangolo LBC ha angolo
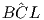 = γ, l’angolo
= γ, l’angolo  = β da cui l’angolo
= β da cui l’angolo 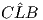 = π – β – γ. Per il teorema dei seni
= π – β – γ. Per il teorema dei seni 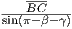 =
=  , da cui (ricordando che sin(π – β – γ) = sin(β + γ)) si ottiene BC = l
, da cui (ricordando che sin(π – β – γ) = sin(β + γ)) si ottiene BC = l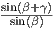 .Non corretto
.Non corretto
Soluzione: C. Per risolvere tale quesito è necessario ricordare che sin(π – α) = sin(α) ed il teorema dei seni, secondo cui in ogni triangolo ogni lato è proporzionale al seno dell’angolo opposto. Nel triangolo considerato è necessario tracciare la bisettrice a Ĉ che incontra il lato AB in L, formando il segmento CL = l. Il triangolo LBC ha angolo
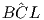 = γ, l’angolo
= γ, l’angolo  = β da cui l’angolo
= β da cui l’angolo 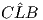 = π – β – γ. Per il teorema dei seni
= π – β – γ. Per il teorema dei seni 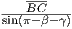 =
=  , da cui (ricordando che sin(π – β – γ) = sin(β + γ)) si ottiene BC = l
, da cui (ricordando che sin(π – β – γ) = sin(β + γ)) si ottiene BC = l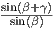 .Risposta non fornita
.Risposta non fornita
Soluzione: C. Per risolvere tale quesito è necessario ricordare che sin(π – α) = sin(α) ed il teorema dei seni, secondo cui in ogni triangolo ogni lato è proporzionale al seno dell’angolo opposto. Nel triangolo considerato è necessario tracciare la bisettrice a Ĉ che incontra il lato AB in L, formando il segmento CL = l. Il triangolo LBC ha angolo
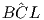 = γ, l’angolo
= γ, l’angolo  = β da cui l’angolo
= β da cui l’angolo 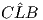 = π – β – γ. Per il teorema dei seni
= π – β – γ. Per il teorema dei seni 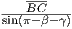 =
=  , da cui (ricordando che sin(π – β – γ) = sin(β + γ)) si ottiene BC = l
, da cui (ricordando che sin(π – β – γ) = sin(β + γ)) si ottiene BC = l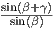 .
. -
Domanda 4 di 8
4. Domanda
L’equazione log x(4) + log 4(x) = -2 è:
Corretto
Soluzione: A. Per la proprietà del cambio di base del logaritmo si ha log a(b) =
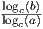 , da cui l’equazione può essere riscritta come
, da cui l’equazione può essere riscritta come 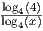 + log 4(x) = -2. Sostituiamo per chiarezza log 4(x) = t, in tal modo otteniamo 1⁄t + t = -2, ovvero
+ log 4(x) = -2. Sostituiamo per chiarezza log 4(x) = t, in tal modo otteniamo 1⁄t + t = -2, ovvero  = 0. Prima di tutto imponiamo il denominatore diverso da 0, ovvero t≠0, da cui log 4(x)≠0, quindi x≠1.
= 0. Prima di tutto imponiamo il denominatore diverso da 0, ovvero t≠0, da cui log 4(x)≠0, quindi x≠1.
A questo punto studiamo t2 + 2t + 1 = 0; si noti che essa può essere riscritta come (t + 1)2 = 0, da cui t = -1. Risostituendo con il logaritmo si ha log 4(x) = -1. Ricordando che alog a(b) = b, allora 4log 4(x) = 4–1, da cui x = 4–1 = 1⁄4. Tale risultato può essere ottenuto anche sostituendo le soluzioni proposte dal quesito all’interno dell’equazione di partenza.Non corretto
Soluzione: A. Per la proprietà del cambio di base del logaritmo si ha log a(b) =
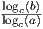 , da cui l’equazione può essere riscritta come
, da cui l’equazione può essere riscritta come 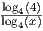 + log 4(x) = -2. Sostituiamo per chiarezza log 4(x) = t, in tal modo otteniamo 1⁄t + t = -2, ovvero
+ log 4(x) = -2. Sostituiamo per chiarezza log 4(x) = t, in tal modo otteniamo 1⁄t + t = -2, ovvero  = 0. Prima di tutto imponiamo il denominatore diverso da 0, ovvero t≠0, da cui log 4(x)≠0, quindi x≠1.
= 0. Prima di tutto imponiamo il denominatore diverso da 0, ovvero t≠0, da cui log 4(x)≠0, quindi x≠1.
A questo punto studiamo t2 + 2t + 1 = 0; si noti che essa può essere riscritta come (t + 1)2 = 0, da cui t = -1. Risostituendo con il logaritmo si ha log 4(x) = -1. Ricordando che alog a(b) = b, allora 4log 4(x) = 4–1, da cui x = 4–1 = 1⁄4. Tale risultato può essere ottenuto anche sostituendo le soluzioni proposte dal quesito all’interno dell’equazione di partenza.Risposta non fornita
Soluzione: A. Per la proprietà del cambio di base del logaritmo si ha log a(b) =
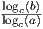 , da cui l’equazione può essere riscritta come
, da cui l’equazione può essere riscritta come 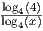 + log 4(x) = -2. Sostituiamo per chiarezza log 4(x) = t, in tal modo otteniamo 1⁄t + t = -2, ovvero
+ log 4(x) = -2. Sostituiamo per chiarezza log 4(x) = t, in tal modo otteniamo 1⁄t + t = -2, ovvero  = 0. Prima di tutto imponiamo il denominatore diverso da 0, ovvero t≠0, da cui log 4(x)≠0, quindi x≠1.
= 0. Prima di tutto imponiamo il denominatore diverso da 0, ovvero t≠0, da cui log 4(x)≠0, quindi x≠1.
A questo punto studiamo t2 + 2t + 1 = 0; si noti che essa può essere riscritta come (t + 1)2 = 0, da cui t = -1. Risostituendo con il logaritmo si ha log 4(x) = -1. Ricordando che alog a(b) = b, allora 4log 4(x) = 4–1, da cui x = 4–1 = 1⁄4. Tale risultato può essere ottenuto anche sostituendo le soluzioni proposte dal quesito all’interno dell’equazione di partenza. -
Domanda 5 di 8
5. Domanda
Una sola fra le seguenti disequazioni ammette un unico numero reale come soluzione. Quale?
Corretto
Soluzione: D. Prima di iniziare bisogna ricordare che il valore assoluto di un polinomio è sempre maggiore o uguale a 0 (uguale a zero quando il suo argomento è nullo). Analizziamo ciascuna delle disequazioni proposte:
- Essendo in valore assoluto, la disequazione proposta è sempre avverata tranne quando si annulla, ossia x≠ – 3;
- Notiamo che un valore non può mai essere negativo ma, al più, nullo. Imponendo quindi l’uguaglianza si trovano due soluzioni: x = ±
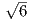 ;
; - In questo caso bisogna analizzare i casi in cui x ≥ 1 e x < 1. Nel primo caso, l’equazione associata è x – 1 + 1 – x > 0, quindi mai verificata. Nel secondo caso, l’equazione associata è -x+1-1+x > 0, ed ancora mai verificata. Per cui l’equazione non ammette soluzioni;
- La quarta disequazione può essere riscritta come 3|x + 1| ≤ 0. Come nel secondo caso, il valore assoluto può essere al più uguale a 0, quando il suo argomento lo è. In tal caso si trova come soluzione x = -1, ossia un unico numero reale;
- Non essendo mai negativo, l’ultima disequazione non è mai verificata.
Non corretto
Soluzione: D. Prima di iniziare bisogna ricordare che il valore assoluto di un polinomio è sempre maggiore o uguale a 0 (uguale a zero quando il suo argomento è nullo). Analizziamo ciascuna delle disequazioni proposte:
- Essendo in valore assoluto, la disequazione proposta è sempre avverata tranne quando si annulla, ossia x≠ – 3;
- Notiamo che un valore non può mai essere negativo ma, al più, nullo. Imponendo quindi l’uguaglianza si trovano due soluzioni: x = ±
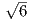 ;
; - In questo caso bisogna analizzare i casi in cui x ≥ 1 e x < 1. Nel primo caso, l’equazione associata è x – 1 + 1 – x > 0, quindi mai verificata. Nel secondo caso, l’equazione associata è -x+1-1+x > 0, ed ancora mai verificata. Per cui l’equazione non ammette soluzioni;
- La quarta disequazione può essere riscritta come 3|x + 1| ≤ 0. Come nel secondo caso, il valore assoluto può essere al più uguale a 0, quando il suo argomento lo è. In tal caso si trova come soluzione x = -1, ossia un unico numero reale;
- Non essendo mai negativo, l’ultima disequazione non è mai verificata.
Risposta non fornita
Soluzione: D. Prima di iniziare bisogna ricordare che il valore assoluto di un polinomio è sempre maggiore o uguale a 0 (uguale a zero quando il suo argomento è nullo). Analizziamo ciascuna delle disequazioni proposte:
- Essendo in valore assoluto, la disequazione proposta è sempre avverata tranne quando si annulla, ossia x≠ – 3;
- Notiamo che un valore non può mai essere negativo ma, al più, nullo. Imponendo quindi l’uguaglianza si trovano due soluzioni: x = ±
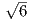 ;
; - In questo caso bisogna analizzare i casi in cui x ≥ 1 e x < 1. Nel primo caso, l’equazione associata è x – 1 + 1 – x > 0, quindi mai verificata. Nel secondo caso, l’equazione associata è -x+1-1+x > 0, ed ancora mai verificata. Per cui l’equazione non ammette soluzioni;
- La quarta disequazione può essere riscritta come 3|x + 1| ≤ 0. Come nel secondo caso, il valore assoluto può essere al più uguale a 0, quando il suo argomento lo è. In tal caso si trova come soluzione x = -1, ossia un unico numero reale;
- Non essendo mai negativo, l’ultima disequazione non è mai verificata.
-
Domanda 6 di 8
6. Domanda
Dato un sistema di assi ortogonali Oxy, è data la semicirconferenza y =
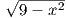 . Qual è il suo raggio?Corretto
. Qual è il suo raggio?Corretto
Soluzione: D. Ricordiamo che una circonferenza con centro nell’origine ha forma x2 + y2 = r2, dove r è il raggio. La circonferenza riportata non è espressa in forma canonica. Per riportarla nella forma considerata, eleviamo entrambi i membri al quadrato, trovando y2 = 9 – x2, ossia x2 + y2 = 9. Se ne deduce che r2 = 9, ovvero r = 3.
Non corretto
Soluzione: D. Ricordiamo che una circonferenza con centro nell’origine ha forma x2 + y2 = r2, dove r è il raggio. La circonferenza riportata non è espressa in forma canonica. Per riportarla nella forma considerata, eleviamo entrambi i membri al quadrato, trovando y2 = 9 – x2, ossia x2 + y2 = 9. Se ne deduce che r2 = 9, ovvero r = 3.
Risposta non fornita
Soluzione: D. Ricordiamo che una circonferenza con centro nell’origine ha forma x2 + y2 = r2, dove r è il raggio. La circonferenza riportata non è espressa in forma canonica. Per riportarla nella forma considerata, eleviamo entrambi i membri al quadrato, trovando y2 = 9 – x2, ossia x2 + y2 = 9. Se ne deduce che r2 = 9, ovvero r = 3.
-
Domanda 7 di 8
7. Domanda
Sia b = 4005. Allora si ha:
Corretto
Soluzione: C. Per affrontare questi esercizi è necessario ricordare che 1024 = 210 ≃ 103 = 1000. In tal caso riscriviamo b come (4 × 100)5 = (22 × 102)5 = 210 × 1010. Essendo le soluzioni proposte espresse in base 10 ricordiamo che 210 ≃ 103, per cui 210 × 1010 ≃ 103 × 1010 = 1013. Vediamo che 1013 è tra la soluzione B e la C. Ciononostante, analizzando l’approssimazione fatta, notiamo che 210 > 103 per cui b > 1013 ma non molto più grande, da cui si conclude la C.
Non corretto
Soluzione: C. Per affrontare questi esercizi è necessario ricordare che 1024 = 210 ≃ 103 = 1000. In tal caso riscriviamo b come (4 × 100)5 = (22 × 102)5 = 210 × 1010. Essendo le soluzioni proposte espresse in base 10 ricordiamo che 210 ≃ 103, per cui 210 × 1010 ≃ 103 × 1010 = 1013. Vediamo che 1013 è tra la soluzione B e la C. Ciononostante, analizzando l’approssimazione fatta, notiamo che 210 > 103 per cui b > 1013 ma non molto più grande, da cui si conclude la C.
Risposta non fornita
Soluzione: C. Per affrontare questi esercizi è necessario ricordare che 1024 = 210 ≃ 103 = 1000. In tal caso riscriviamo b come (4 × 100)5 = (22 × 102)5 = 210 × 1010. Essendo le soluzioni proposte espresse in base 10 ricordiamo che 210 ≃ 103, per cui 210 × 1010 ≃ 103 × 1010 = 1013. Vediamo che 1013 è tra la soluzione B e la C. Ciononostante, analizzando l’approssimazione fatta, notiamo che 210 > 103 per cui b > 1013 ma non molto più grande, da cui si conclude la C.
-
Domanda 8 di 8
8. Domanda
Fissato nel piano un sistema di riferimento cartesiano ortogonale Oxy, quale delle seguenti è una parabola con asse parallelo all’asse delle x?
Corretto
Soluzione: D. Si ricordi che una parabola con asse parallelo ad asse delle ordinate (y) ha forma y = ax2 + bx + c con a≠0. Affinché essa abbia asse parallelo a quello delle ascisse, è sufficiente sostituire le x con le y (e viceversa) all’interno dell’equazione, ovvero x = ay2 + by + c.
Si noti che la prima equazione rappresenta una parabola con asse parallelo alle ordinate. La seconda non rappresenta una parabola in quanto sia la x sia la y compaiono al secondo grado.
La terza equazione proposta rappresenta una retta, mentre la quarta è bene una parabola con asse parallelo alle ascisse. Infatti quest’ultima può essere espressa come x = 4y2 – 4y + 3. Infine, l’ultima equazione può essere riscritta come x = , ovvero una retta parallela all’asse delle ordinate.Non corretto
, ovvero una retta parallela all’asse delle ordinate.Non corretto
Soluzione: D. Si ricordi che una parabola con asse parallelo ad asse delle ordinate (y) ha forma y = ax2 + bx + c con a≠0. Affinché essa abbia asse parallelo a quello delle ascisse, è sufficiente sostituire le x con le y (e viceversa) all’interno dell’equazione, ovvero x = ay2 + by + c.
Si noti che la prima equazione rappresenta una parabola con asse parallelo alle ordinate. La seconda non rappresenta una parabola in quanto sia la x sia la y compaiono al secondo grado.
La terza equazione proposta rappresenta una retta, mentre la quarta è bene una parabola con asse parallelo alle ascisse. Infatti quest’ultima può essere espressa come x = 4y2 – 4y + 3. Infine, l’ultima equazione può essere riscritta come x = , ovvero una retta parallela all’asse delle ordinate.Risposta non fornita
, ovvero una retta parallela all’asse delle ordinate.Risposta non fornita
Soluzione: D. Si ricordi che una parabola con asse parallelo ad asse delle ordinate (y) ha forma y = ax2 + bx + c con a≠0. Affinché essa abbia asse parallelo a quello delle ascisse, è sufficiente sostituire le x con le y (e viceversa) all’interno dell’equazione, ovvero x = ay2 + by + c.
Si noti che la prima equazione rappresenta una parabola con asse parallelo alle ordinate. La seconda non rappresenta una parabola in quanto sia la x sia la y compaiono al secondo grado.
La terza equazione proposta rappresenta una retta, mentre la quarta è bene una parabola con asse parallelo alle ascisse. Infatti quest’ultima può essere espressa come x = 4y2 – 4y + 3. Infine, l’ultima equazione può essere riscritta come x = , ovvero una retta parallela all’asse delle ordinate.
, ovvero una retta parallela all’asse delle ordinate.
TIL Comprensione Verbale – Demo
0 di 5 domande completate
Domande:
- 1
- 2
- 3
- 4
- 5
Informazione
Stai per iniziare la simulazione della sezione di Comprensione del testo e Logica del TIL-I (Test in Laib – Ingegneria) del Politecnico di Torino.
Questa versione dimostrativa si compone di 5 domande da svolgere in 10 minuti.
Ti ricordiamo che invece la prova completa di Comprensione del testo e Logica del TIL-I dura 20 minuti ed è composta da 10 domande.
Puoi esercitarti con le simulazioni complete e le correzioni dettagliate del Corso Completo TIL POLITO
Durante la prova potrai rivedere le domande a cui hai già dato risposta. Allo scadere del tempo, il test si concluderà automaticamente mostrandoti le risposte ai quesiti.
Assicurati di essere in un ambiente tranquillo in quanto non sarà possibile interrompere lo svolgimento se non terminando e iniziando nuovamente la prova.
Premi il tasto sottostante per iniziare la prova.
Hai già completato il quiz pertanto non puoi rifarlo.
Il quiz si sta caricando…
Devi iscriverti o registrarti per iniziare il quiz.
Bisogna completare il seguente quiz per poter avviare questo quiz:
Risultati
0 di 5 domande risposte correttamente
Il tuo tempo:
Il tempo è scaduto
Punteggio finale: 0
Risposte fornite: 0
Risposte corrette: 0 con punteggio 0
Risposte non corrette: 0 con penalità 0
-
Comprensione Verbale
Risposte fornite: 0
Risposte corrette: 0 con punteggio 0
Risposte non corrette: 0 con punteggio 0
-
Logica
Risposte fornite: 0
Risposte corrette: 0 con punteggio 0
Risposte non corrette: 0 con punteggio 0
-
Vuoi metterti alla prova con altre simulazioni per prepararti e ripassare ciò che c’è da sapere per superare rapidamente l’esame? Continua ad esercitarti con le simulazioni complete e le correzioni dettagliate:
Vai al Corso Completo TIL POLITO
Leggi le opinioni degli altri studenti o contattaci per qualsiasi informazione. Consulta anche la pagina dei Codici Sconto per verificare le promozioni disponibili.
Premi il tasto sottostante per vedere le correzioni.
- 1
- 2
- 3
- 4
- 5
- Risposta
- Controlla
-
Domanda 1 di 5
1. Domanda
Categoria: Comprensione VerbaleLa relatività ai mezzi di osservazione
Ogni microoggetto si manifesta nell’interazione con l’apparecchio di osservazione. Ad esempio, la traiettoria di una particella diventa visibile soltanto in seguito al processo irreversibile a mo’ di valanga nella camera di Wilson o in uno strato di lastra fotografica (e durante questo processo la particella perde energia nella ionizzazione dell’aria o del fotostrato, cosicché la sua quantità di moto diventa indefinita). Il risultato dell’interazione di un oggetto atomico con un apparecchio descritto in modo classico è, dunque, l’elemento sperimentale fondamentale, la cui sistematizzazione sulla base di queste o quelle supposizioni circa le proprietà dell’oggetto costituisce compito della teoria: dalla analisi di tali interazioni vengono dedotte le proprietà dell’oggetto atomico, e le predizioni della teoria vengono formulate come quei risultati delle interazioni, che ci si deve attendere.
Una simile impostazione del problema autorizza pienamente l’introduzione di grandezze, che descrivono l’oggetto di per sé, indipendentemente dall’apparecchio (carica, massa, spin della particella e anche altre proprietà dell’oggetto, descritte da operatori quantistici), ma nello stesso tempo consente vari tipi di approcci all’oggetto; l’oggetto può venire caratterizzato mediante quelle sue proprietà (ad esempio, corpuscolari od ondulatorie) che si manifestano in relazione all’apparecchio di misura e alle condizioni esterne da esso create.
La nuova impostazione del problema consente di considerare il caso in cui differenti aspetti e diverse proprietà dell’oggetto non si manifestano contemporaneamente, cioè il caso in cui non sia possibile una descrizione particolareggiata del comportamento dell’oggetto.
La situazione si presenterà in questi termini se differenti proprietà dell’oggetto (ad esempio, l’attitudine di un elettrone ad essere localizzato nello spazio e la sua attitudine all’interferenza) esigono condizioni esterne fra loro incompatibili.
Secondo la proposta di Bohr, si possono chiamare complementari quelle proprietà, che si manifestano (in forma netta) soltanto in condizioni tra loro incompatibili, e che in condizioni attuabili appaiono soltanto parzialmente, in una forma «attenuata» (ad esempio, la localizzazione approssimata, ammessa dalle disuguaglianze di Heisenberg, nello spazio delle coordinate e in quello degli impulsi). Prendere in considerazione una manifestazione simultanea di proprietà complementari (nella loro forma netta) non ha senso: ciò spiega anche il fatto che non sia contraddittoria la nozione di «dualismo corpuscolare-ondulatorio».
Ponendo alla base del nuovo metodo di descrizione i risultati dell’interazione fra il microoggetto e l’apparecchio noi, con ciò, introduciamo l’importante concetto di relatività ai mezzi di osservazione, che costituisce una generalizzazione dell’ormai da lungo tempo noto concetto di relatività al sistema di riferimento. Un tale metodo di descrizione non significa affatto che noi consideriamo l’oggetto qualcosa di meno reale dell’apparecchio, o che noi riduciamo le proprietà dell’oggetto a quelle dell’apparecchio. Al contrario, la descrizione sulla base del concetto di relatività ai mezzi di osservazione fornisce una descrizione del microoggetto senz’altro più profonda e precisa, di quanto non fosse possibile sulla base delle idealizzazioni della fisica classica. Una simile descrizione richiede anche un apparato matematico più elaborato, e cioè la teoria degli operatori lineari, dei loro autovalori e delle loro autofunzioni, la teoria dei gruppi e altri concetti matematici. L’applicazione di tale apparato ai problemi della fisica quantistica ha consentito di fornire una spiegazione teorica di una serie di proprietà fondamentali della materia, che non possono venir chiarite sulla base di nozioni classiche. Ma oltre a ciò, cosa non meno importante per noi, l’interpretazione fisica dei concetti matematici impiegati in tale apparato conduce ad alcune conclusioni generali di grande interesse, in particolare alla generalizzazione del concetto di stato di un sistema sulla base delle nozioni di probabilità e di possibilità potenziale.1) Posizione e impulso:
Corretto
Soluzione: A. Si legge nel testo: “che si manifestano (in forma netta) soltanto in condizioni tra loro incompatibili, e che in condizioni attuabili appaiono soltanto parzialmente, in una forma «attenuata» (ad esempio, la localizzazione approssimata, ammessa dalle disuguaglianze di Heisenberg, nello spazio delle coordinate e in quello degli impulsi)”. Da cui si deduce che Posizione e impulso sono localizzabili contemporaneamente solo in forma approssimata.
Non corretto
Soluzione: A. Si legge nel testo: “che si manifestano (in forma netta) soltanto in condizioni tra loro incompatibili, e che in condizioni attuabili appaiono soltanto parzialmente, in una forma «attenuata» (ad esempio, la localizzazione approssimata, ammessa dalle disuguaglianze di Heisenberg, nello spazio delle coordinate e in quello degli impulsi)”. Da cui si deduce che Posizione e impulso sono localizzabili contemporaneamente solo in forma approssimata.
Risposta non fornita
Soluzione: A. Si legge nel testo: “che si manifestano (in forma netta) soltanto in condizioni tra loro incompatibili, e che in condizioni attuabili appaiono soltanto parzialmente, in una forma «attenuata» (ad esempio, la localizzazione approssimata, ammessa dalle disuguaglianze di Heisenberg, nello spazio delle coordinate e in quello degli impulsi)”. Da cui si deduce che Posizione e impulso sono localizzabili contemporaneamente solo in forma approssimata.
-
Domanda 2 di 5
2. Domanda
Categoria: Comprensione Verbale2) Oggetto della fisica quantistica:
Corretto
Soluzione: D. Leggiamo nel testo che “Una simile impostazione del problema autorizza pienamente l’introduzione di grandezze, che descrivono l’oggetto di per sé, indipendentemente dall’apparecchio (carica, massa, spin della particella e anche altre proprietà dell’oggetto, descritte da operatori quantistici)”, da cui la risposta D è quella corretta.
Non corretto
Soluzione: D. Leggiamo nel testo che “Una simile impostazione del problema autorizza pienamente l’introduzione di grandezze, che descrivono l’oggetto di per sé, indipendentemente dall’apparecchio (carica, massa, spin della particella e anche altre proprietà dell’oggetto, descritte da operatori quantistici)”, da cui la risposta D è quella corretta.
Risposta non fornita
Soluzione: D. Leggiamo nel testo che “Una simile impostazione del problema autorizza pienamente l’introduzione di grandezze, che descrivono l’oggetto di per sé, indipendentemente dall’apparecchio (carica, massa, spin della particella e anche altre proprietà dell’oggetto, descritte da operatori quantistici)”, da cui la risposta D è quella corretta.
-
Domanda 3 di 5
3. Domanda
Categoria: LogicaDomanda 3
Assumendo che sia vera l’affermazione “Se uno studente studia, verrà promosso all’esame”, quale delle seguenti affermazioni è vera?
Corretto
Soluzione: B. Studiare è sufficiente, ma non necessario per essere promosso. Dunque, se uno studente viene promosso potrebbe aver studiato, ma non è necessario. Per cui la risposta corretta è la B.
Non corretto
Soluzione: B. Studiare è sufficiente, ma non necessario per essere promosso. Dunque, se uno studente viene promosso potrebbe aver studiato, ma non è necessario. Per cui la risposta corretta è la B.
Risposta non fornita
Soluzione: B. Studiare è sufficiente, ma non necessario per essere promosso. Dunque, se uno studente viene promosso potrebbe aver studiato, ma non è necessario. Per cui la risposta corretta è la B.
-
Domanda 4 di 5
4. Domanda
Categoria: LogicaDomanda 4
In un sacchetto ci sono alcune biglie.
Adele dice: “Nel sacchetto ci sono in tutto tre biglie e sono nere”.
Barbara dice: “Nel sacchetto ci sono due biglie nere e due biglie rosse”.
Carla dice: “Nel sacchetto ci sono solo biglie nere”.
Sapendo che uno solo dei tre ha mentito, quante biglie ci sono nel sacchetto?
Corretto
Soluzione: C. Sapendo che una sola persona ha mentito, possiamo supporre che una persona per volta mente. Partiamo da Adele, se mente allora vuol dire che nel sacchetto non ci sono tre biglie e non sono tutte nere. Ma in tal caso allora anche Carla mentirebbe in quanto dice che ci sono solo biglie nere.
Sapendo che solo una persona mente, allora non può essere Adele perché ci porterebbe alla conclusione che due persone mentono.
Di conseguenza neanche Carla sta mentendo, per cui l’unica persone che mente è Barbara.
Dato che Adele non mente allora, per quanto detto da Adele, ci sono 3 biglie nel sacchetto.Non corretto
Soluzione: C. Sapendo che una sola persona ha mentito, possiamo supporre che una persona per volta mente. Partiamo da Adele, se mente allora vuol dire che nel sacchetto non ci sono tre biglie e non sono tutte nere. Ma in tal caso allora anche Carla mentirebbe in quanto dice che ci sono solo biglie nere.
Sapendo che solo una persona mente, allora non può essere Adele perché ci porterebbe alla conclusione che due persone mentono.
Di conseguenza neanche Carla sta mentendo, per cui l’unica persone che mente è Barbara.
Dato che Adele non mente allora, per quanto detto da Adele, ci sono 3 biglie nel sacchetto.Risposta non fornita
Soluzione: C. Sapendo che una sola persona ha mentito, possiamo supporre che una persona per volta mente. Partiamo da Adele, se mente allora vuol dire che nel sacchetto non ci sono tre biglie e non sono tutte nere. Ma in tal caso allora anche Carla mentirebbe in quanto dice che ci sono solo biglie nere.
Sapendo che solo una persona mente, allora non può essere Adele perché ci porterebbe alla conclusione che due persone mentono.
Di conseguenza neanche Carla sta mentendo, per cui l’unica persone che mente è Barbara.
Dato che Adele non mente allora, per quanto detto da Adele, ci sono 3 biglie nel sacchetto. -
Domanda 5 di 5
5. Domanda
Categoria: LogicaDomanda 5
Quanti sono i numeri naturali di quattro cifre in cui compare una e una sola volta la cifra 5 ed essa è la cifra più grande presente nel numero?
Corretto
Soluzione: A. Se 5 è la cifra più grande e compare una e una sola volta, allora le altre cifre possibili sono 0, 1, 2, 3 e 4 (5 cifre).
Nel caso 5 sia in prima cifra, ci sono altre 3 cifre da scegliere. Per ciascun posto ci sono 5 possibilità, quindi vi sono 5x5x5 = 125 numeri.
Nel caso in cui 5 si trovi alla seconda cifra, al primo posto non potremo mettere lo 0, perché equivarrebbe a un numero di 3 cifre. Quindi le possibilità per la prima cifra si riducono a 4, mentre per la terza e la quarta abbiamo 5 cifre possibili, per un totale di 4x5x5 = 100 numeri.
Lo stesso ragionamento sopra può essere fatto nel caso il 5 si trovi alla terza o alla quarta cifra.
Contando i numeri possibili abbiamo 125+100+100+100 = 425 (risposta A).Non corretto
Soluzione: A. Se 5 è la cifra più grande e compare una e una sola volta, allora le altre cifre possibili sono 0, 1, 2, 3 e 4 (5 cifre).
Nel caso 5 sia in prima cifra, ci sono altre 3 cifre da scegliere. Per ciascun posto ci sono 5 possibilità, quindi vi sono 5x5x5 = 125 numeri.
Nel caso in cui 5 si trovi alla seconda cifra, al primo posto non potremo mettere lo 0, perché equivarrebbe a un numero di 3 cifre. Quindi le possibilità per la prima cifra si riducono a 4, mentre per la terza e la quarta abbiamo 5 cifre possibili, per un totale di 4x5x5 = 100 numeri.
Lo stesso ragionamento sopra può essere fatto nel caso il 5 si trovi alla terza o alla quarta cifra.
Contando i numeri possibili abbiamo 125+100+100+100 = 425 (risposta A).Risposta non fornita
Soluzione: A. Se 5 è la cifra più grande e compare una e una sola volta, allora le altre cifre possibili sono 0, 1, 2, 3 e 4 (5 cifre).
Nel caso 5 sia in prima cifra, ci sono altre 3 cifre da scegliere. Per ciascun posto ci sono 5 possibilità, quindi vi sono 5x5x5 = 125 numeri.
Nel caso in cui 5 si trovi alla seconda cifra, al primo posto non potremo mettere lo 0, perché equivarrebbe a un numero di 3 cifre. Quindi le possibilità per la prima cifra si riducono a 4, mentre per la terza e la quarta abbiamo 5 cifre possibili, per un totale di 4x5x5 = 100 numeri.
Lo stesso ragionamento sopra può essere fatto nel caso il 5 si trovi alla terza o alla quarta cifra.
Contando i numeri possibili abbiamo 125+100+100+100 = 425 (risposta A).
TIL Fisica – Demo
0 di 5 domande completate
Domande:
- 1
- 2
- 3
- 4
- 5
Informazione
Stai per iniziare la simulazione della sezione di Fisica del TIL-I (Test in Laib – Ingegneria) del Politecnico di Torino.
Questa versione dimostrativa si compone di 5 domande da svolgere in 11 minuti.
Ti ricordiamo che invece la prova completa di Fisica del TIL-I dura 22 minuti ed è composta da 10 domande.
Puoi esercitarti con le simulazioni complete e le correzioni dettagliate del Corso Completo TIL POLITO
Durante la prova potrai rivedere le domande a cui hai già dato risposta. Allo scadere del tempo, il test si concluderà automaticamente mostrandoti le risposte ai quesiti.
Assicurati di essere in un ambiente tranquillo in quanto non sarà possibile interrompere lo svolgimento se non terminando e iniziando nuovamente la prova.
Premi il tasto sottostante per iniziare la prova.
Hai già completato il quiz pertanto non puoi rifarlo.
Il quiz si sta caricando…
Devi iscriverti o registrarti per iniziare il quiz.
Bisogna completare il seguente quiz per poter avviare questo quiz:
Risultati
Il tuo tempo:
Il tempo è scaduto
Punteggio finale: 0
Risposte fornite: 0
Risposte corrette: 0 con punteggio 0
Risposte non corrette: 0 con penalità 0
| Punteggio medio |
|
| Il tuo punteggio |
|
-
Non categorizzato
Risposte fornite: 0
Risposte corrette: 0 con punteggio 0
Risposte non corrette: 0 con punteggio 0
-
Vuoi metterti alla prova con altre simulazioni per prepararti e ripassare ciò che c’è da sapere per superare rapidamente l’esame? Continua ad esercitarti con le simulazioni complete e le correzioni dettagliate:
Vai al Corso Completo TIL POLITO
Leggi le opinioni degli altri studenti o contattaci per qualsiasi informazione. Consulta anche la pagina dei Codici Sconto per verificare le promozioni disponibili.
Premi il tasto sottostante per vedere le correzioni.
- 1
- 2
- 3
- 4
- 5
- Risposta
- Controlla
-
Domanda 1 di 5
1. Domanda
In uno ione negativo:
Corretto
Soluzione: C. In generale si ricordi che: il numero di protoni nel nucleo (particelle subatomiche di segno positivo) indica l’elemento, il numero di neutroni, di segno nullo, nel nucleo ne indica l’isotopo (elementi uguali ma con diverse proprietà) mentre il numero di elettroni, particelle subatomiche di segno negativo non poste nel nucleo, può variare. In particolare, quando il numero di protoni è pari al numero di elettroni, l’atomo è neutro in quanto le cariche negative sono bilanciate da un numero pari di cariche positive. Un squilibrio nel numero porta alla formazione di ioni negativi o positivi. In uno ione negativo il numero di cariche negative è superiore a quello di cariche positive, ovvero il numero di elettroni è superiore a quello dei protoni, da cui la risposta C è quella esatta.
Non corretto
Soluzione: C. In generale si ricordi che: il numero di protoni nel nucleo (particelle subatomiche di segno positivo) indica l’elemento, il numero di neutroni, di segno nullo, nel nucleo ne indica l’isotopo (elementi uguali ma con diverse proprietà) mentre il numero di elettroni, particelle subatomiche di segno negativo non poste nel nucleo, può variare. In particolare, quando il numero di protoni è pari al numero di elettroni, l’atomo è neutro in quanto le cariche negative sono bilanciate da un numero pari di cariche positive. Un squilibrio nel numero porta alla formazione di ioni negativi o positivi. In uno ione negativo il numero di cariche negative è superiore a quello di cariche positive, ovvero il numero di elettroni è superiore a quello dei protoni, da cui la risposta C è quella esatta.
Risposta non fornita
Soluzione: C. In generale si ricordi che: il numero di protoni nel nucleo (particelle subatomiche di segno positivo) indica l’elemento, il numero di neutroni, di segno nullo, nel nucleo ne indica l’isotopo (elementi uguali ma con diverse proprietà) mentre il numero di elettroni, particelle subatomiche di segno negativo non poste nel nucleo, può variare. In particolare, quando il numero di protoni è pari al numero di elettroni, l’atomo è neutro in quanto le cariche negative sono bilanciate da un numero pari di cariche positive. Un squilibrio nel numero porta alla formazione di ioni negativi o positivi. In uno ione negativo il numero di cariche negative è superiore a quello di cariche positive, ovvero il numero di elettroni è superiore a quello dei protoni, da cui la risposta C è quella esatta.
-
Domanda 2 di 5
2. Domanda
Quale dei seguenti enunciati è falso, secondo la fisica classica?
Corretto
Soluzione: D. Benché in un sistema isolato l’energia si conservi, essa può trasformarsi, passando quindi da energia cinetica ad un altro tipo e viceversa. Per esempio, se consideriamo la caduta di un oggetto, esso guadagna energia cinetica durante la caduta, portando l’energia cinetica del sistema ad aumentare.
Non corretto
Soluzione: D. Benché in un sistema isolato l’energia si conservi, essa può trasformarsi, passando quindi da energia cinetica ad un altro tipo e viceversa. Per esempio, se consideriamo la caduta di un oggetto, esso guadagna energia cinetica durante la caduta, portando l’energia cinetica del sistema ad aumentare.
Risposta non fornita
Soluzione: D. Benché in un sistema isolato l’energia si conservi, essa può trasformarsi, passando quindi da energia cinetica ad un altro tipo e viceversa. Per esempio, se consideriamo la caduta di un oggetto, esso guadagna energia cinetica durante la caduta, portando l’energia cinetica del sistema ad aumentare.
-
Domanda 3 di 5
3. Domanda
La costante di Planck, anche detta quanto d’azione e indicata con h, è una costante fisica che rappresenta l’azione minima possibile, o elementare. Essa viene introdotta per quantificare l’energia E trasportata da un’onda elettromagnetica con frequenza costante v nella seguente formula: E = nhν con n = 0,1,2,3,….
Qual è l’unità di grandezza della costante di Planck?Corretto
Soluzione: B. Analizziamo le grandezze che intervengono nell’espressione. A sinistra dell’uguale abbiamo solo l’energia, che ha come grandezza i Joule (J). A destra abbiamo invece tre grandezze: h stessa, la frequenza v di dimensione s-1 e n che è adimensionale (come si può dedurre dai valori interi adimensionali che assume).
Riscrivendo l’espressione in termini dimensionali si ha J = s-1 × [h], dove [h] indica l’unità di misura di h. Si trova che [h] = J × s. Tale grandezza non è presente tra quelle elencate, ciononostante sappiamo che W = J⁄S, quindi W × s2 = J⁄S × s2 = J × s. Da cui la risposta B è quella corretta.Non corretto
Soluzione: B. Analizziamo le grandezze che intervengono nell’espressione. A sinistra dell’uguale abbiamo solo l’energia, che ha come grandezza i Joule (J). A destra abbiamo invece tre grandezze: h stessa, la frequenza v di dimensione s-1 e n che è adimensionale (come si può dedurre dai valori interi adimensionali che assume).
Riscrivendo l’espressione in termini dimensionali si ha J = s-1 × [h], dove [h] indica l’unità di misura di h. Si trova che [h] = J × s. Tale grandezza non è presente tra quelle elencate, ciononostante sappiamo che W = J⁄S, quindi W × s2 = J⁄S × s2 = J × s. Da cui la risposta B è quella corretta.Risposta non fornita
Soluzione: B. Analizziamo le grandezze che intervengono nell’espressione. A sinistra dell’uguale abbiamo solo l’energia, che ha come grandezza i Joule (J). A destra abbiamo invece tre grandezze: h stessa, la frequenza v di dimensione s-1 e n che è adimensionale (come si può dedurre dai valori interi adimensionali che assume).
Riscrivendo l’espressione in termini dimensionali si ha J = s-1 × [h], dove [h] indica l’unità di misura di h. Si trova che [h] = J × s. Tale grandezza non è presente tra quelle elencate, ciononostante sappiamo che W = J⁄S, quindi W × s2 = J⁄S × s2 = J × s. Da cui la risposta B è quella corretta. -
Domanda 4 di 5
4. Domanda
Sapendo che la caloria è l’energia necessaria per far passare un grammo d’acqua da una temperatura di 14.5° a 15.5° e che una caloria corrisponde a circa 4,2 J (ovvero il calore specifico dell’acqua è 4,2JK-1g-1), in quanti secondi un fornello che eroga una potenza pari a 500 W e con un’efficienza pari al 30% riesce a portare una pentola contenente 2 litri d’acqua da 300 K a 370 K?
Corretto
Soluzione: A. L’energia necessaria a far aumentare un kilo d’acqua (ovvero un litro) di un grado è pari a 4200J (ovvero ha un calore specifico di 4,2 JK-1g-1). Per aumentare 2 litri d’acqua di 70 gradi, servono allora 4200J × 2kg × 70K = 588000J (in generale si ricordi che per far aumentare di x gradi y grammi di materiale serve un’energia pari a cpxy dove cp è il calore specifico). Siamo però in presenza di efficienza non pari a 100% ma a 30%, ovvero per ogni 10 J erogati, 7 sono dissipati. Per far acquisire 588000 Joule, è necessario erogarne 588000⁄0,3 = 1960000J. Sapendo che la potenza è definita come il rapporto tra energia e tempo in cui essa è erogata, il tempo necessario per avere una certa quantità di energia è dato da t = E⁄P, si ha quindi t =
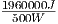 = 3920 secondi.Non corretto
= 3920 secondi.Non corretto
Soluzione: A. L’energia necessaria a far aumentare un kilo d’acqua (ovvero un litro) di un grado è pari a 4200J (ovvero ha un calore specifico di 4,2 JK-1g-1). Per aumentare 2 litri d’acqua di 70 gradi, servono allora 4200J × 2kg × 70K = 588000J (in generale si ricordi che per far aumentare di x gradi y grammi di materiale serve un’energia pari a cpxy dove cp è il calore specifico). Siamo però in presenza di efficienza non pari a 100% ma a 30%, ovvero per ogni 10 J erogati, 7 sono dissipati. Per far acquisire 588000 Joule, è necessario erogarne 588000⁄0,3 = 1960000J. Sapendo che la potenza è definita come il rapporto tra energia e tempo in cui essa è erogata, il tempo necessario per avere una certa quantità di energia è dato da t = E⁄P, si ha quindi t =
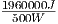 = 3920 secondi.Risposta non fornita
= 3920 secondi.Risposta non fornita
Soluzione: A. L’energia necessaria a far aumentare un kilo d’acqua (ovvero un litro) di un grado è pari a 4200J (ovvero ha un calore specifico di 4,2 JK-1g-1). Per aumentare 2 litri d’acqua di 70 gradi, servono allora 4200J × 2kg × 70K = 588000J (in generale si ricordi che per far aumentare di x gradi y grammi di materiale serve un’energia pari a cpxy dove cp è il calore specifico). Siamo però in presenza di efficienza non pari a 100% ma a 30%, ovvero per ogni 10 J erogati, 7 sono dissipati. Per far acquisire 588000 Joule, è necessario erogarne 588000⁄0,3 = 1960000J. Sapendo che la potenza è definita come il rapporto tra energia e tempo in cui essa è erogata, il tempo necessario per avere una certa quantità di energia è dato da t = E⁄P, si ha quindi t =
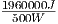 = 3920 secondi.
= 3920 secondi. -
Domanda 5 di 5
5. Domanda
Per camminare lungo una strada orizzontale (con spostamento non nullo), l’attrito tra piedi e suolo è:
Corretto
Soluzione: A. La presenza dell’attrito è necessario per evitare fenomeni di “scivolamento”. Infatti, più l’attrito con il suolo diminuisce (per esempio su una superficie ghiacciata), più la nostra capacità di spostamento diminuisce. L’attrito con il suolo è quindi necessario, indipendentemente dal mezzo in cui ci muoviamo. Infatti, anche nel vuoto, l’attrito con una superficie permette di appoggiarsi e applicare una spinta. In assenza di attrito, la spinta non si genererebbe.Non corretto
Soluzione: A. La presenza dell’attrito è necessario per evitare fenomeni di “scivolamento”. Infatti, più l’attrito con il suolo diminuisce (per esempio su una superficie ghiacciata), più la nostra capacità di spostamento diminuisce. L’attrito con il suolo è quindi necessario, indipendentemente dal mezzo in cui ci muoviamo. Infatti, anche nel vuoto, l’attrito con una superficie permette di appoggiarsi e applicare una spinta. In assenza di attrito, la spinta non si genererebbe.
Risposta non fornita
Soluzione: A. La presenza dell’attrito è necessario per evitare fenomeni di “scivolamento”. Infatti, più l’attrito con il suolo diminuisce (per esempio su una superficie ghiacciata), più la nostra capacità di spostamento diminuisce. L’attrito con il suolo è quindi necessario, indipendentemente dal mezzo in cui ci muoviamo. Infatti, anche nel vuoto, l’attrito con una superficie permette di appoggiarsi e applicare una spinta. In assenza di attrito, la spinta non si genererebbe.
TIL Conoscenze Tecniche – Demo
0 di 3 domande completate
Domande:
- 1
- 2
- 3
Informazione
Stai per iniziare la simulazione della sezione di Conoscenze tecniche di base del TIL-I (Test in Laib – Ingegneria) del Politecnico di Torino.
Questa versione dimostrativa si compone di 3 domande da svolgere in 6 minuti.
Ti ricordiamo che invece la prova completa di Conoscenze tecniche di base del TIL-I dura 12 minuti ed è composta da 6 domande.
Puoi esercitarti con le simulazioni complete e le correzioni dettagliate del Corso Completo TIL POLITO
Durante la prova potrai rivedere le domande a cui hai già dato risposta. Allo scadere del tempo, il test si concluderà automaticamente mostrandoti le risposte ai quesiti.
Assicurati di essere in un ambiente tranquillo in quanto non sarà possibile interrompere lo svolgimento se non terminando e iniziando nuovamente la prova.
Premi il tasto sottostante per iniziare la prova.
Hai già completato il quiz pertanto non puoi rifarlo.
Il quiz si sta caricando…
Devi iscriverti o registrarti per iniziare il quiz.
Bisogna completare il seguente quiz per poter avviare questo quiz:
Risultati
Il tuo tempo:
Il tempo è scaduto
Punteggio finale: 0
Risposte fornite: 0
Risposte corrette: 0 con punteggio 0
Risposte non corrette: 0 con penalità 0
| Punteggio medio |
|
| Il tuo punteggio |
|
-
Non categorizzato
Risposte fornite: 0
Risposte corrette: 0 con punteggio 0
Risposte non corrette: 0 con punteggio 0
-
Vuoi metterti alla prova con altre simulazioni per prepararti e ripassare ciò che c’è da sapere per superare rapidamente l’esame? Continua ad esercitarti con le simulazioni complete e le correzioni dettagliate:
Vai al Corso Completo TIL POLITO
Leggi le opinioni degli altri studenti o contattaci per qualsiasi informazione. Consulta anche la pagina dei Codici Sconto per verificare le promozioni disponibili.
Premi il tasto sottostante per vedere le correzioni.
- 1
- 2
- 3
- Risposta
- Controlla
-
Domanda 1 di 3
1. Domanda
Qual è il valore stampato a video (di x + y) al termine del programma?
 Corretto
Corretto
Soluzione: A. La variabile x viene inizializzata a 2 mentre y a x alla terza, cioè 2 alla terza 3 che è uguale a 8. Le variabili entrano in un ciclo for. Si ricordi che ad ogni ciclo la variabile di ciclo i aumenta di 1 partendo da i=1 fino a quando arriva a 3. A ogni ciclo x viene posta uguale y per i. Al primo ciclo, x risulta pari a 8 x 1 = 8. Al secondo ciclo, x viene posta uguale a 8 x 2 = 16. Al terzo e ultimo ciclo, x è pari a 8 x 3 = 24. Uscita dal ciclo, la variabile y viene incrementata di 5, passando quindi da 8 a 13.
A questo punto le variabili passano all’interno di una istruzione condizionale che viene svolta se e solo se x-y < y. Nel nostro caso, sostituendo i valori, 24-13 = 11 < 13, la disuguaglianza è verificata quindi l’istruzione viene eseguita e la variabile x viene incrementata di 3, passando da 24 a 27.
Il valore stampato a video è quindi x+y = 27+13 = 40.Non corretto
Soluzione: A. La variabile x viene inizializzata a 2 mentre y a x alla terza, cioè 2 alla terza 3 che è uguale a 8. Le variabili entrano in un ciclo for. Si ricordi che ad ogni ciclo la variabile di ciclo i aumenta di 1 partendo da i=1 fino a quando arriva a 3. A ogni ciclo x viene posta uguale y per i. Al primo ciclo, x risulta pari a 8 x 1 = 8. Al secondo ciclo, x viene posta uguale a 8 x 2 = 16. Al terzo e ultimo ciclo, x è pari a 8 x 3 = 24. Uscita dal ciclo, la variabile y viene incrementata di 5, passando quindi da 8 a 13.
A questo punto le variabili passano all’interno di una istruzione condizionale che viene svolta se e solo se x-y < y. Nel nostro caso, sostituendo i valori, 24-13 = 11 < 13, la disuguaglianza è verificata quindi l’istruzione viene eseguita e la variabile x viene incrementata di 3, passando da 24 a 27.
Il valore stampato a video è quindi x+y = 27+13 = 40.Risposta non fornita
Soluzione: A. La variabile x viene inizializzata a 2 mentre y a x alla terza, cioè 2 alla terza 3 che è uguale a 8. Le variabili entrano in un ciclo for. Si ricordi che ad ogni ciclo la variabile di ciclo i aumenta di 1 partendo da i=1 fino a quando arriva a 3. A ogni ciclo x viene posta uguale y per i. Al primo ciclo, x risulta pari a 8 x 1 = 8. Al secondo ciclo, x viene posta uguale a 8 x 2 = 16. Al terzo e ultimo ciclo, x è pari a 8 x 3 = 24. Uscita dal ciclo, la variabile y viene incrementata di 5, passando quindi da 8 a 13.
A questo punto le variabili passano all’interno di una istruzione condizionale che viene svolta se e solo se x-y < y. Nel nostro caso, sostituendo i valori, 24-13 = 11 < 13, la disuguaglianza è verificata quindi l’istruzione viene eseguita e la variabile x viene incrementata di 3, passando da 24 a 27.
Il valore stampato a video è quindi x+y = 27+13 = 40. -
Domanda 2 di 3
2. Domanda
Che cos’è un firewall?
Corretto
Soluzione: A. Un firewall è una specie di filtro passivo che controlla il traffico di dati e blocca le trasmissioni pericolose o indesiderate in base a una serie di regole specifiche. La maggior parte dei firewall dispone di norme standard a cui l’utente finale può aggiungere altre personalizzate, in base alle proprie necessità. Il firewall può essere sia hardware sia software.
Non corretto
Soluzione: A. Un firewall è una specie di filtro passivo che controlla il traffico di dati e blocca le trasmissioni pericolose o indesiderate in base a una serie di regole specifiche. La maggior parte dei firewall dispone di norme standard a cui l’utente finale può aggiungere altre personalizzate, in base alle proprie necessità. Il firewall può essere sia hardware sia software.
Risposta non fornita
Soluzione: A. Un firewall è una specie di filtro passivo che controlla il traffico di dati e blocca le trasmissioni pericolose o indesiderate in base a una serie di regole specifiche. La maggior parte dei firewall dispone di norme standard a cui l’utente finale può aggiungere altre personalizzate, in base alle proprie necessità. Il firewall può essere sia hardware sia software.
-
Domanda 3 di 3
3. Domanda
Quale tipo di rappresentazione è utilizzata nella figura?
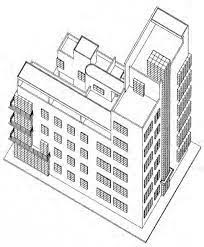 Corretto
Corretto
Soluzione: E. L’edificio rappresentato è in assonometria cavaliera, distinguibile dall’angolo di 90° (e non di 120°, come nell’assonometria ortogonale isometrica) che l’angolo dell’edificio forma.
Non corretto
Soluzione: E. L’edificio rappresentato è in assonometria cavaliera, distinguibile dall’angolo di 90° (e non di 120°, come nell’assonometria ortogonale isometrica) che l’angolo dell’edificio forma.
Risposta non fornita
Soluzione: E. L’edificio rappresentato è in assonometria cavaliera, distinguibile dall’angolo di 90° (e non di 120°, come nell’assonometria ortogonale isometrica) che l’angolo dell’edificio forma.
